Joint with Sudheer Sahu & John Reif
In Proc. Eleventh International Meeting on DNA Computing, 2005, to appear
Downloads: Paper short version: PDF , paper full version: PDF , talk slides: PPT
Abstract: Self-assembly is a process in which small objects
autonomously associate with each other to form larger complexes. It is ubiquitous
in biological constructions at the cellular and molecular scale and has
also been identified by nanoscientists as a fundamental method for building
molecular scale structures. Recent years see convergent interest and efforts
in studying self-assembly from mathematicians, computer scientists, physicists,
chemists, and biologists. However most complexity theoretic studies of self-assembly
utilize mathematical models with two limitations: 1) only attraction, while
no repulsion, is studied; 2) only assembled structures of two dimensional
square grids are studied.
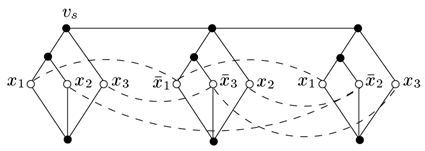
In this paper, we study the complexity of the assemblies resulting
from the cooperative effect of repulsion and attraction in a more general
setting of graphs. This allows for the study of a more general class of
self-assembled structures than the previous tiling model. We define two
novel assembly models, namely the accretive graph assembly model and the
self-destructible graph assembly model, and identify one fundamental problem
in them: the sequential construction of a given graph, referred to as Accretive
Graph Assembly Problem (AGAP) and Self-Destructible Graph Assembly Problem
(DGAP), respectively. Our main results are: (i) AGAP is NP-complete even
if the maximum degree of the graph is restricted to 4 or the graph is restricted
to be planar with maximum degree 5; (ii) counting the number of sequential
assembly orderings that result in a target graph (SAGAP) is SHARPP-complete;
and (iii) DGAP~ is PSPACE-complete even if the maximum degree of the
graph is restricted to 6 (this is the first PSPACE-complete result in self-assembly).
We also extend the accretive graph assembly model to a stochastic model,
and prove that determining the probability of a given assembly in this model
is SHARPP-complete.

Back to
pulications